Threshold regression for time series in Stata 15
In time series analysis, sometimes we are suspicious that relationships among variables might change at some time. The new threshold command allows you to look for these changes in a statistically informed way, which helps you avoid the potential for bias if you just eyeball line charts and pick the point that fits with your expectations.
Here’s a simple example. The goldfinch is a small songbird found throughout Eurasia. In these population data from the United Kingdom, you can see a sudden change in the time series at around 1986.
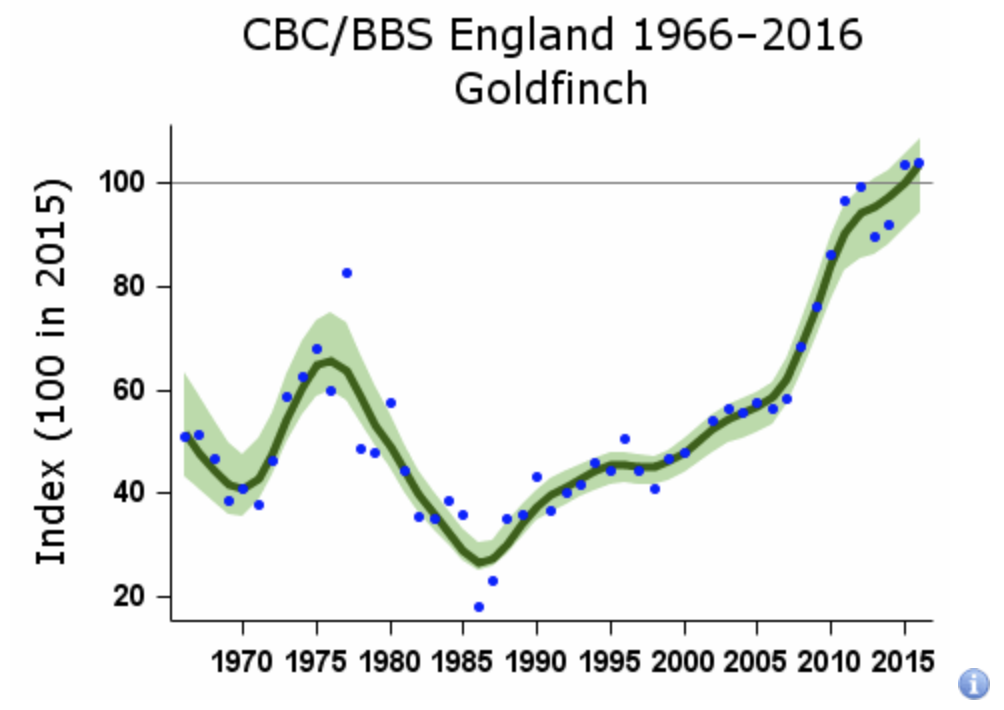
Image copyright British Trust for Ornithology
This is generally ascribed to the birds learning how to forage in suburban gardens. Prior to that point, you might have studied the effect of the size of field margins on farms on the goldfinch population, on the basis that the birds eat seeds of wild plants that grow on the margins of cultivated land. The post-1986 data would throw your analysis out; the birds near human habitation were no longer totally dependent on wild plants. Identifying the threshold and fitting different models on either side allows you to improve causal understanding or prediction.
An example with weather data
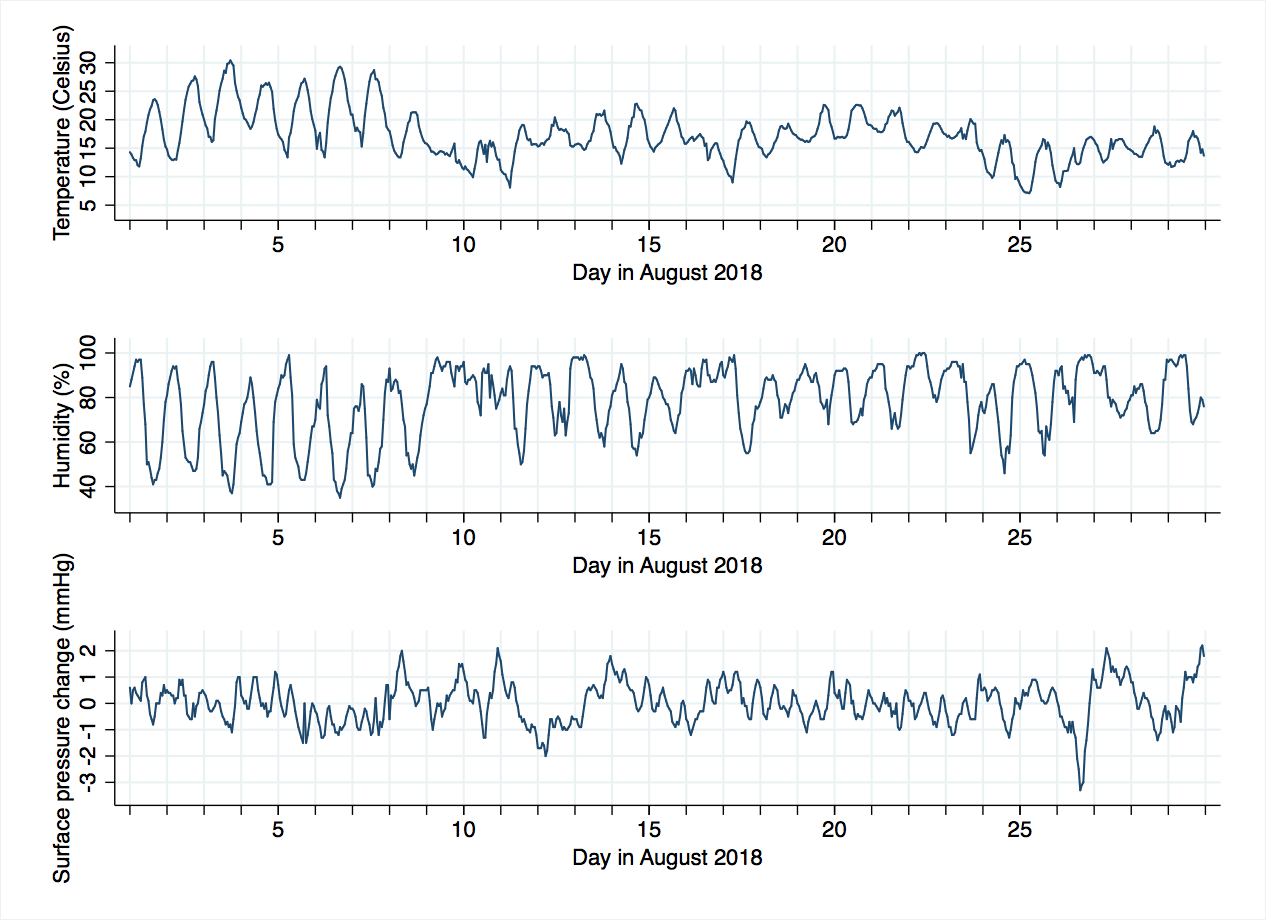
Let’s look at a fairly small dataset: a few weather variables from an observation station to the South of London in August 2018. You can download the data file here.
We will open the file (I suggest you browse it to see what’s inside) and declare it to be a time series.
use "kenley.dta", clear
tsset datetime, clocktime delta(1 hour)
Next, we make two new variables: decimalday will be handy for plotting, and hoursine is a quick and dirty way of incorporating the daily oscillation in temperature, with minimum about 5 a.m. and maximum about 5 p.m., fairly standard in an English summer. We are imposing a sinusoidal shape on this oscillation, and fixing the time of the minimum and maximum, which is not a great idea for time series analysis, but will simplify what follows and allow us to focus on the threshold command.
generate decimalday = day + (hour/24)
generate hoursine = sin((hour-11)/12*3.14)
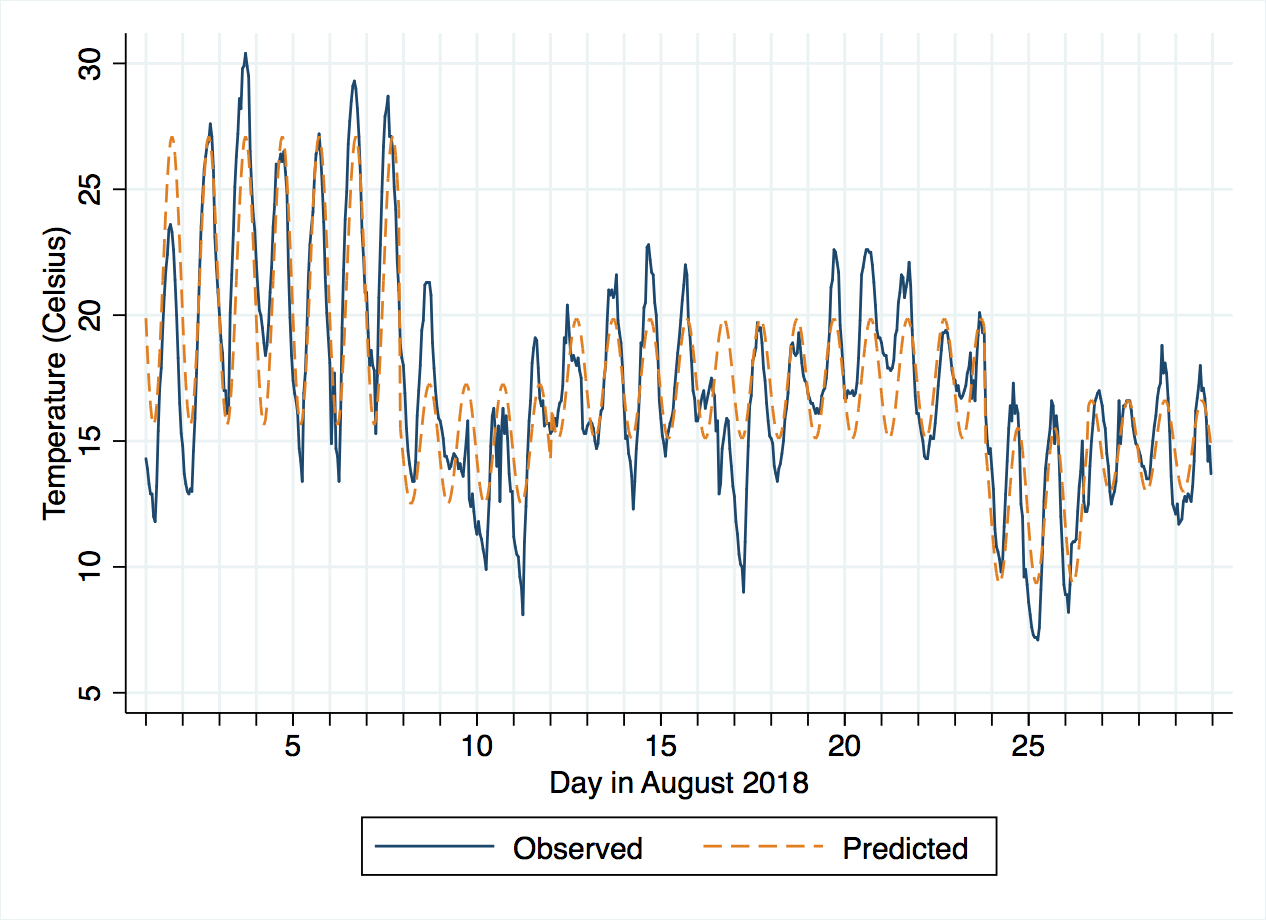
If we regress temperature on hoursine, we can evaluate the size of the diurnal variation. Bear in mind that hoursine varies from -1 to 1, so the coefficient tells us the average change from 5 a.m. to 11 a.m. or 11 a.m. to 5 p.m.
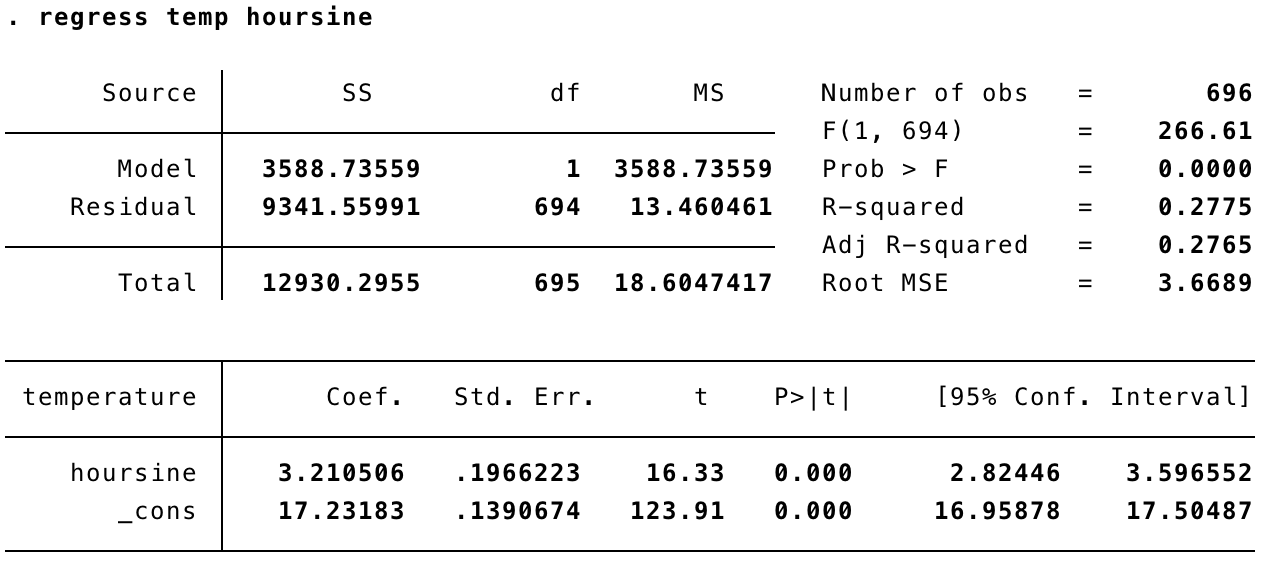
This change is 3.2 degrees Celsius, with 95% confidence interval from 2.8 to 3.6. The intercept term can be interpreted as the average temperature at 11 a.m. (17.2 degrees, confidence interval 17.0 to 17.5). If you compare this to the line chart for temperatures, the size of the sine wave looks fairly sensible, but it is centered around 17 degrees, when actually the month started with temperatures notably above that, which then dropped around the 8th of August to be below that. Looking more closely, the period before the 8th seems to have larger amplitude (height of the wave) than after the 8th. Really, we need to consider at least one threshold point.
To run the corresponding threshold regression, we can simply type threshold temperature, threshvar(decimalday) regionvars(hoursine). threshvar tells Stata which variable to use to detect the threshold location(s) and regionvars tells it what variable(s) will be used as predictors on either side of the threshold(s).
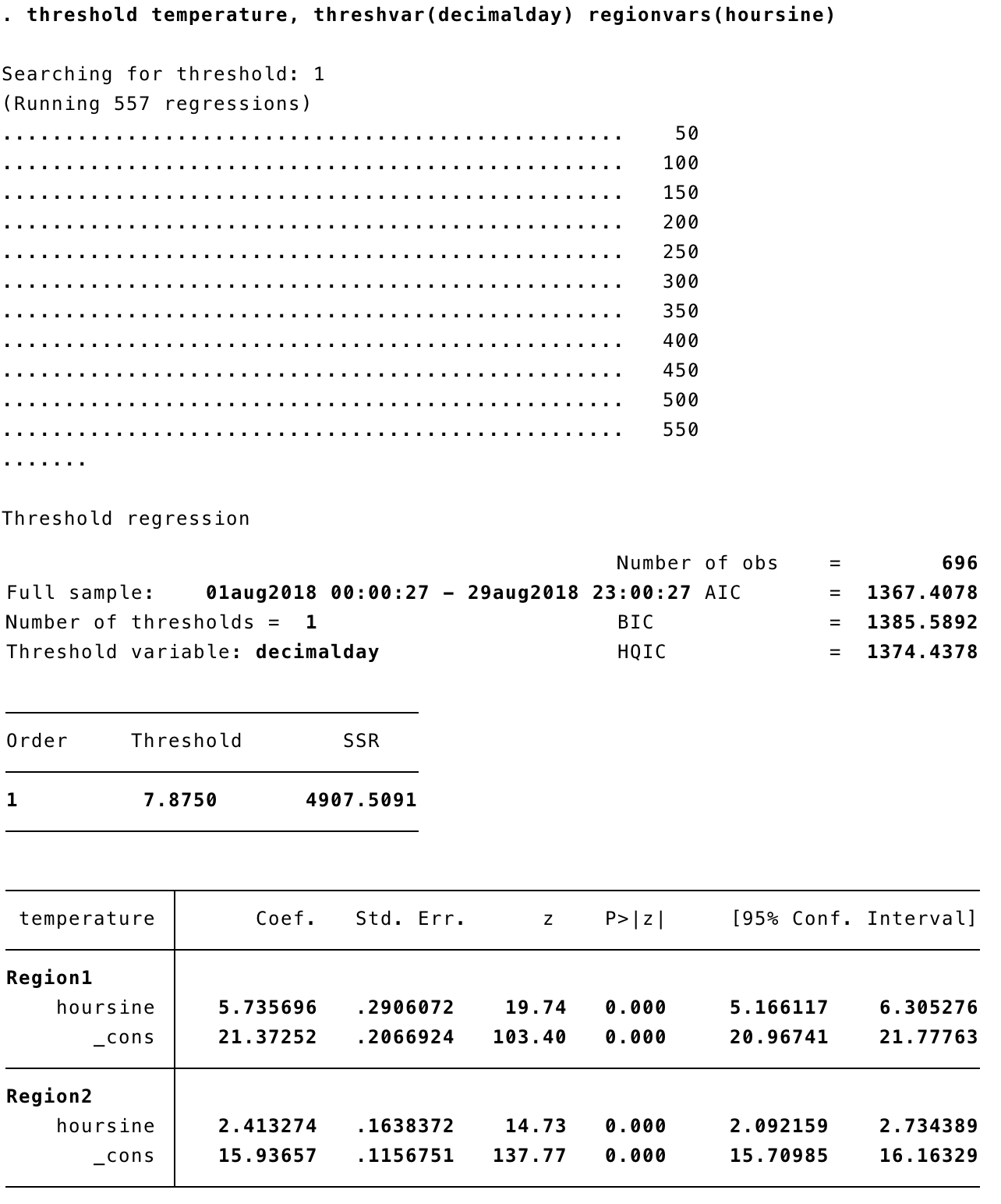
threshold fits linear regressions (I’ll discuss later what you can do in non-Gaussian error situations), and it runs a fairly exhaustive search along the range of threshvar, fitting 557 regressions in this case. Fortunately, linear regressions are fitted by simple matrix algebra and are hence very fast. The default is to look for one threshold, but we will extend that later.
The output includes Akaike information criterion (AIC), Bayesian information criterion (BIC) and Hannan-Quinn information criterion (HQIC); BIC in particular allows inter-model comparisons. This is helpful if you want to compare a model with one threshold to a model with two, for example.
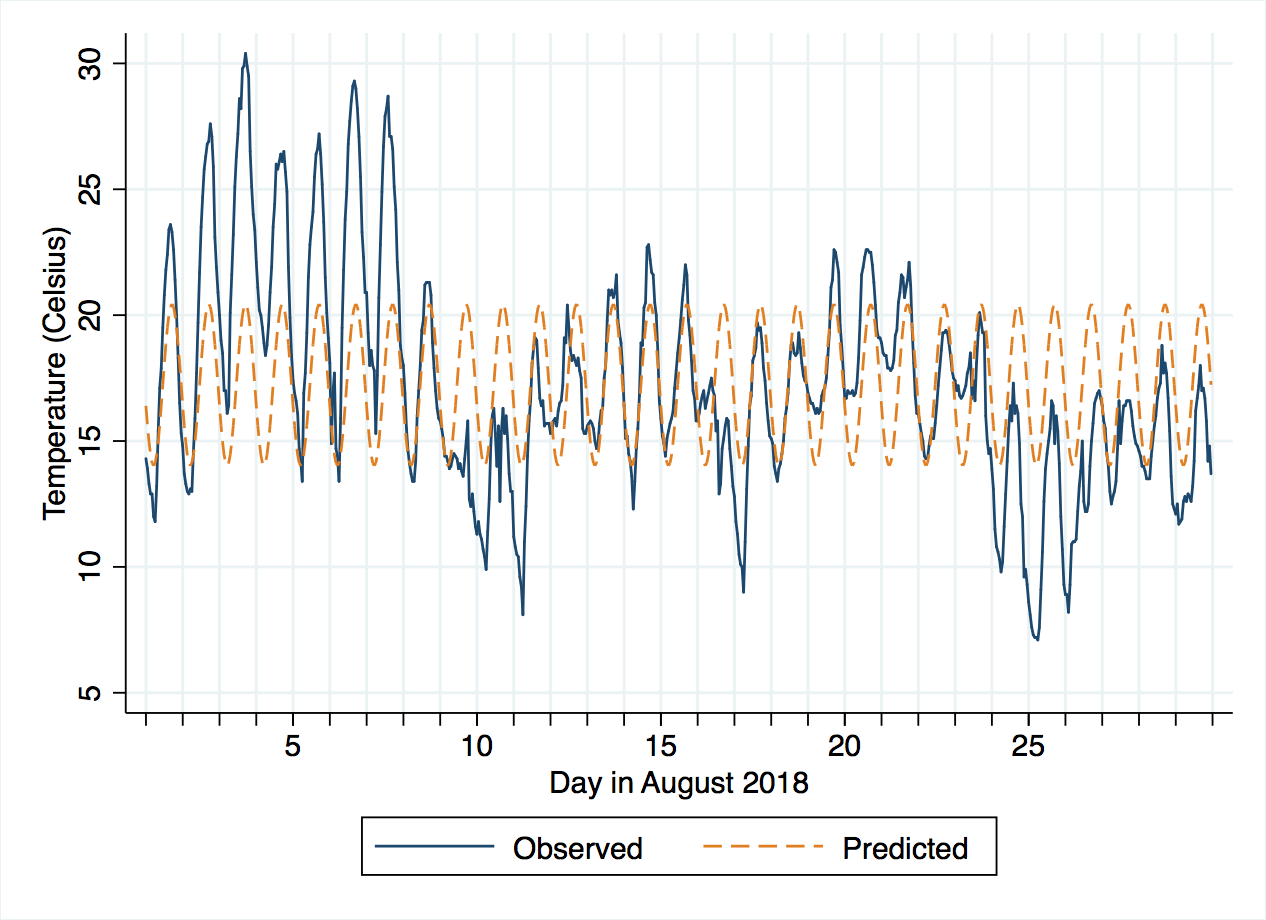
There is also a sum of squared residuals (SSR), which is 4908 for one threshold. We can compare this will the simple regression above, where the sum of squares (SS) residual is 9342 – a big improvement! The threshold itself occurs on the night of 7-8 August (decimalday = 7.875), which is indeed the most obvious changepoint in the time series. In fact, this coincides with a cold front moving over the area after a record-breaking period of hot, dry weather.
Visualising the new model’s predictions, we can see it does much better, although there might be a case for subdividing the period after the 8th further.
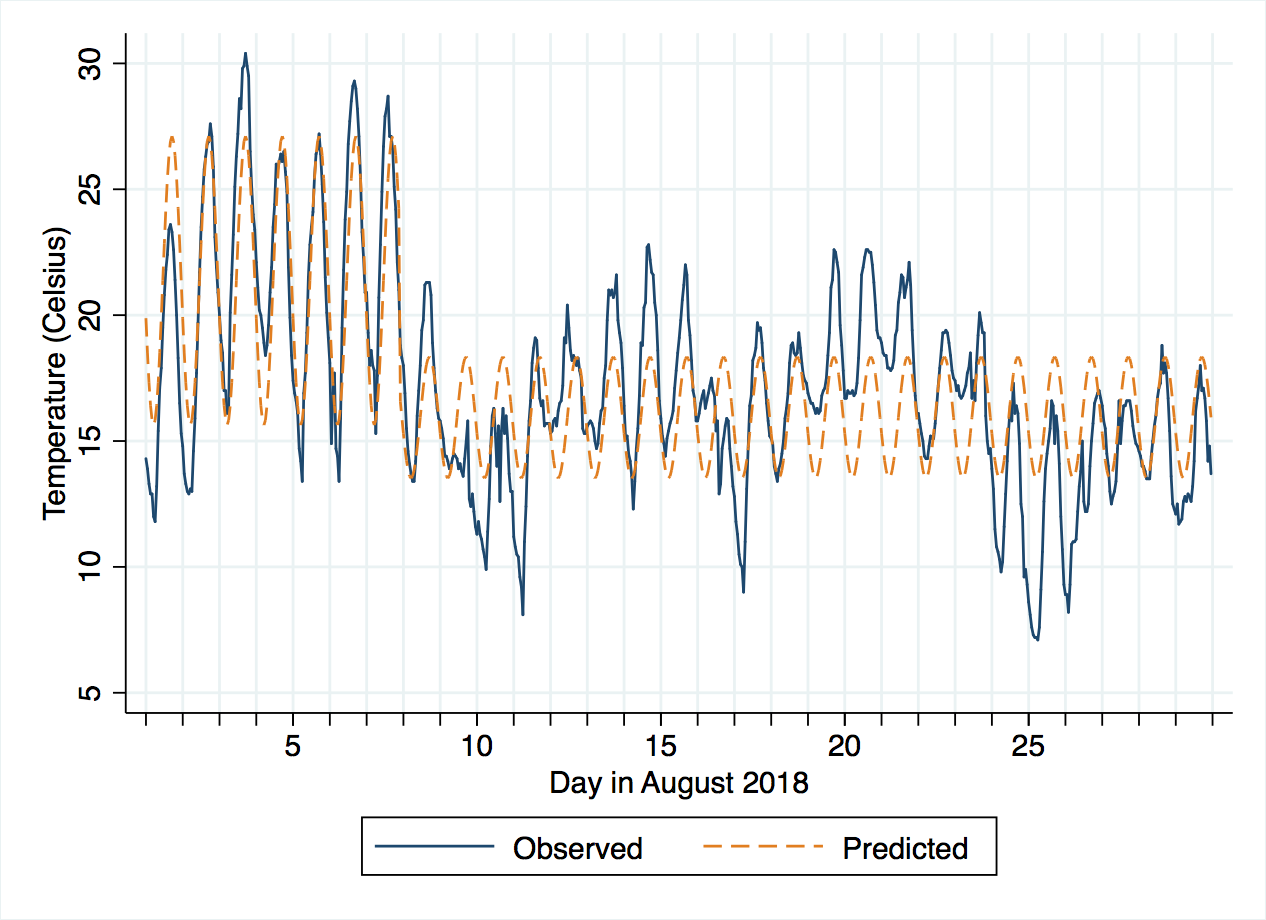
The accompanying do-file shows how the number of thresholds, and their locations, can be extracted into Stata macros and reused, for example in graphics, without hard-coding their values.
More than one threshold
To allow for more thresholds, we can just add the option optthresh(4).
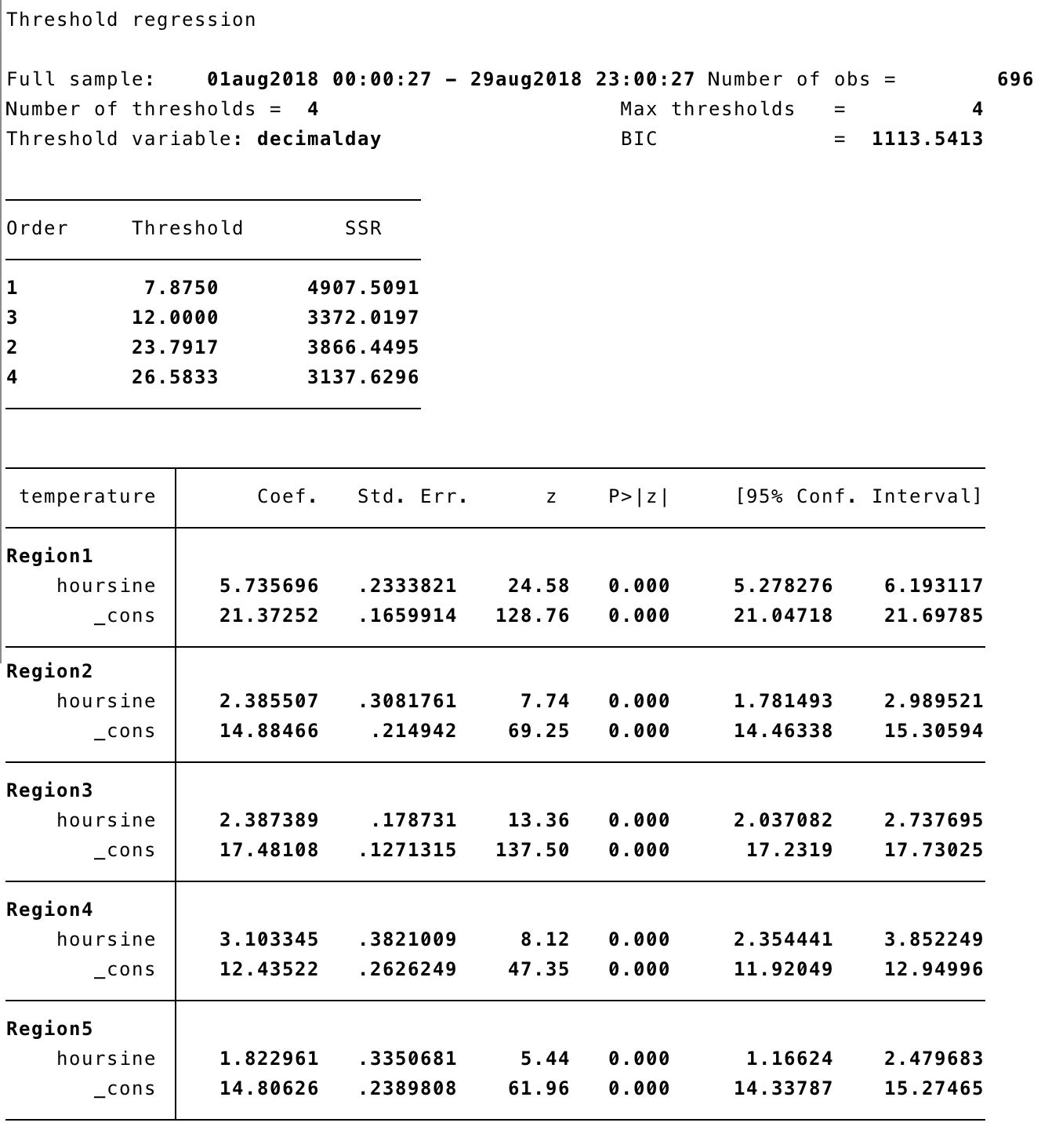
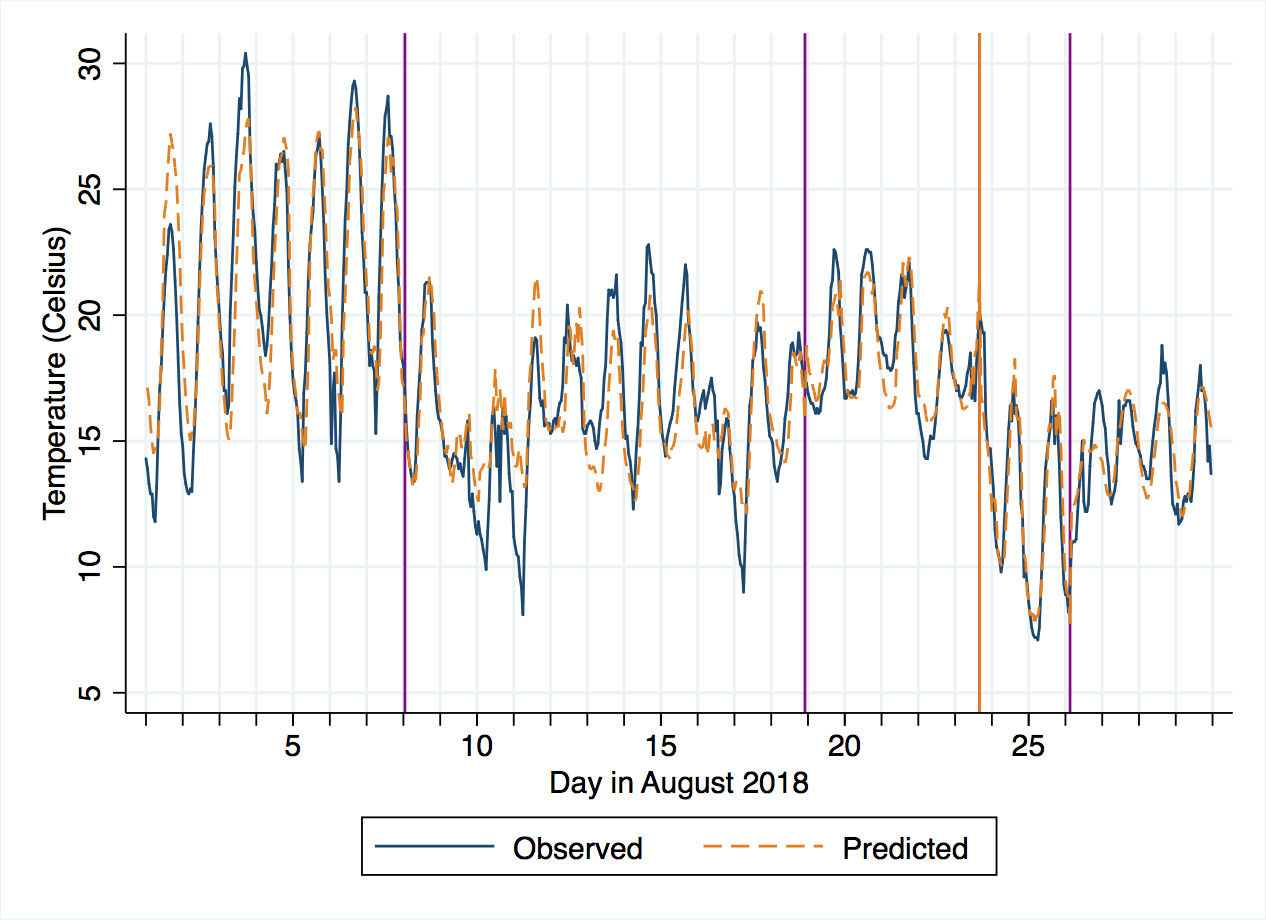
After 4 scans through the data, we get four threshold points. The residual sum of squares is shown as each one is added, ending at 3138 with a BIC of 1114, notably lower than the 1386 of the one-threshold model. The chart below shows their locations in purple, with the one-threshold model’s location in orange (overlapping one of the purple lines).
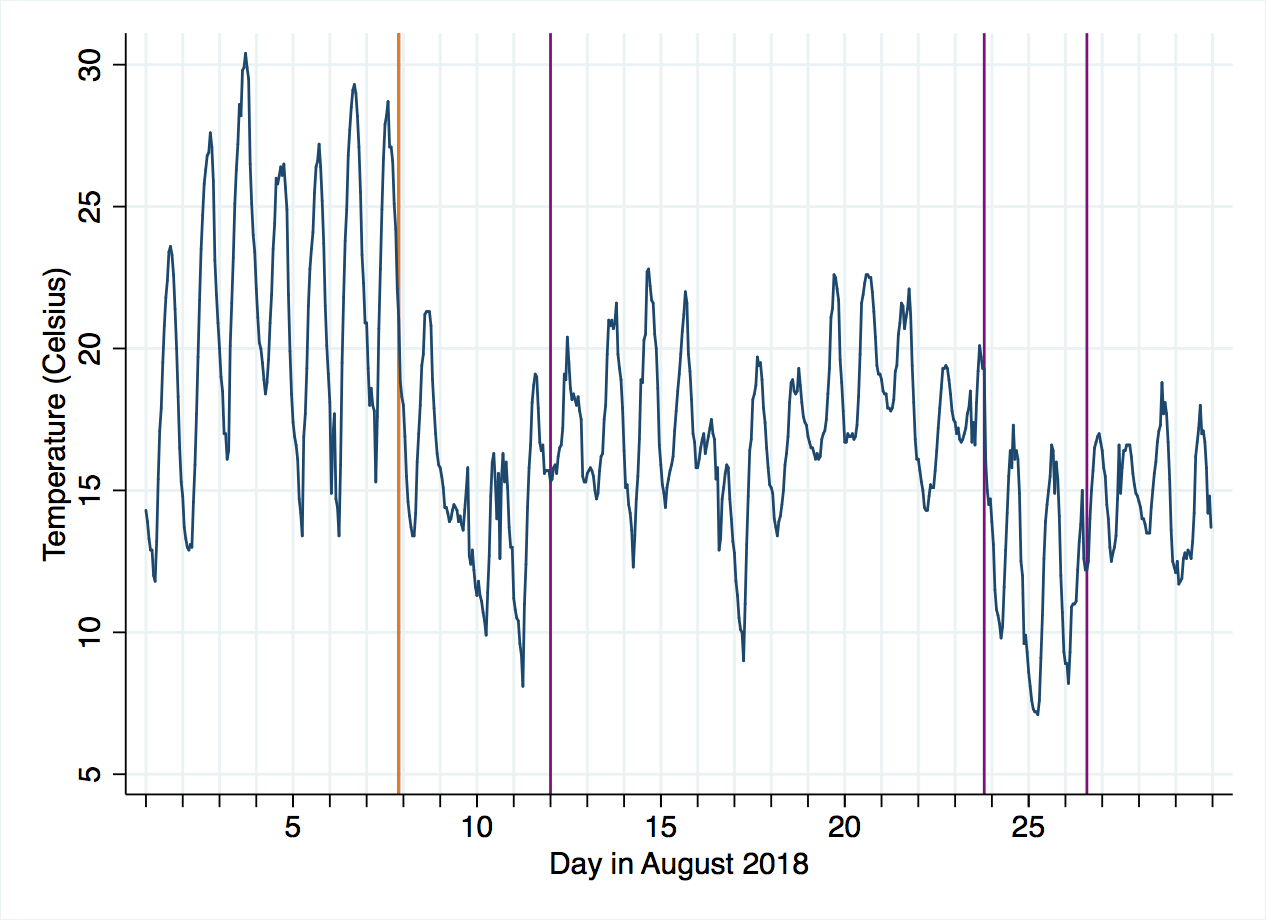
The new model clearly has predctions that more closely follow the observed data, and this is supported by the BIC, although the reduction in residual sum of squares does not always decrease as more thresholds are added, so we should be cautious about adding these additional thresholds. I’ll come back to this point at the end.
Threshold regression with more predictors
Now that we’ve seen the basics of how threshold works, let’s try it out with a more realistic regression. In the weather data, we might want to predict temperature based on hoursine, as well as the lagged values of humidity and pressure_change.
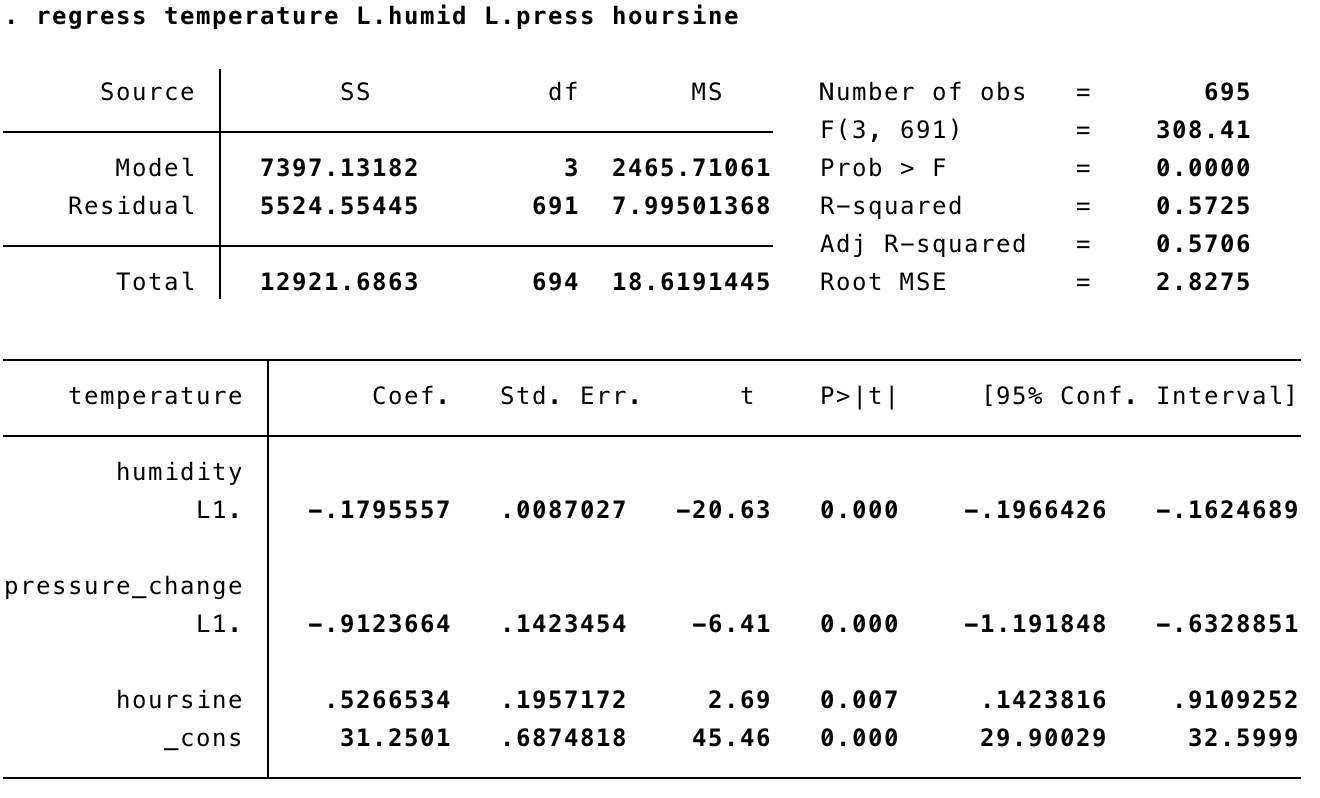
Running threshold with one threshold, we get:
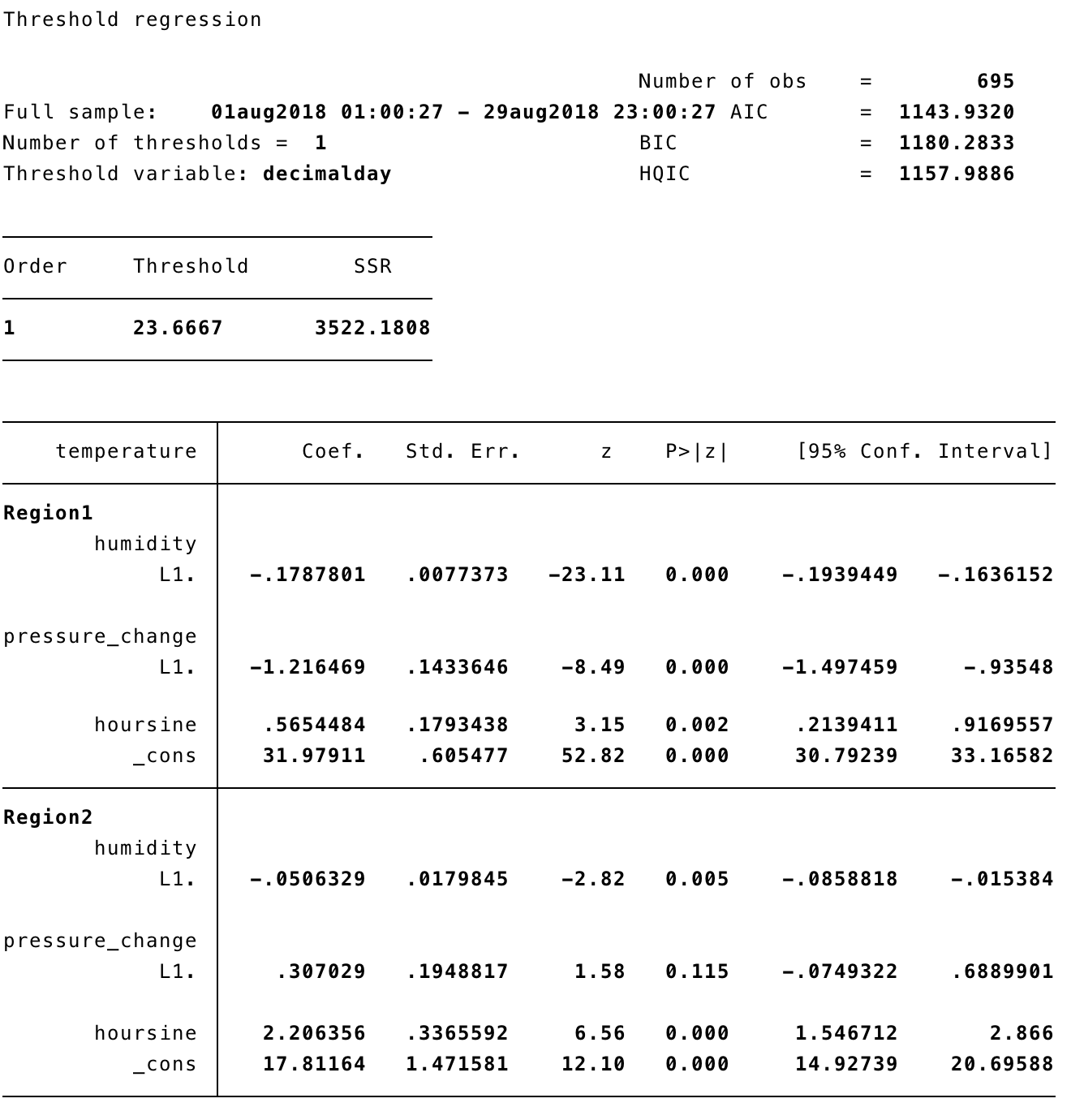
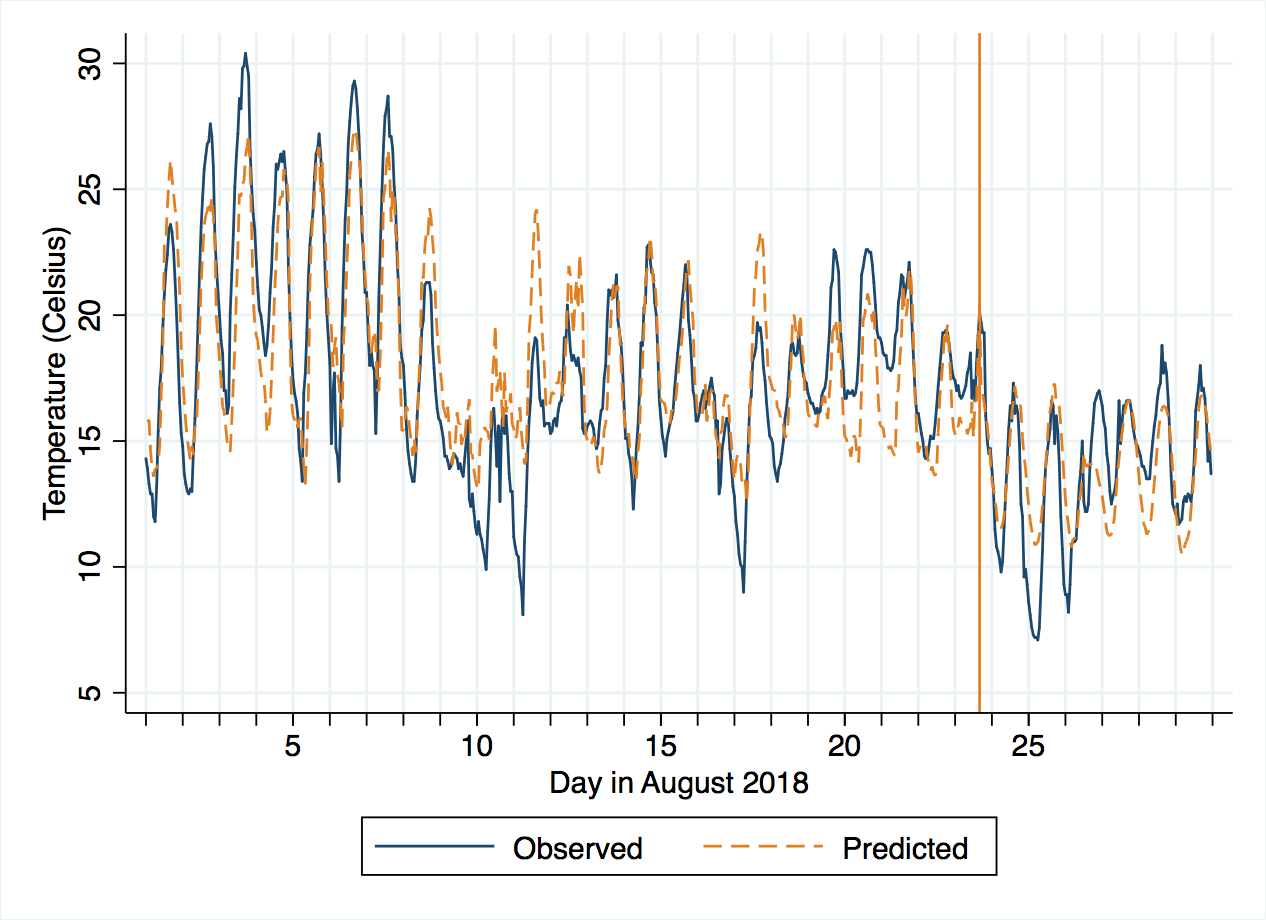
This has put the one threshold much later in the month, probably because the disturbance in temperature around the 8th is adequately predicted by disturbances in humidity and pressure too. The observed and predicted plot looks like there are a couple of short periods of systematic over- or under-estimation.
A four-threshold model follows:
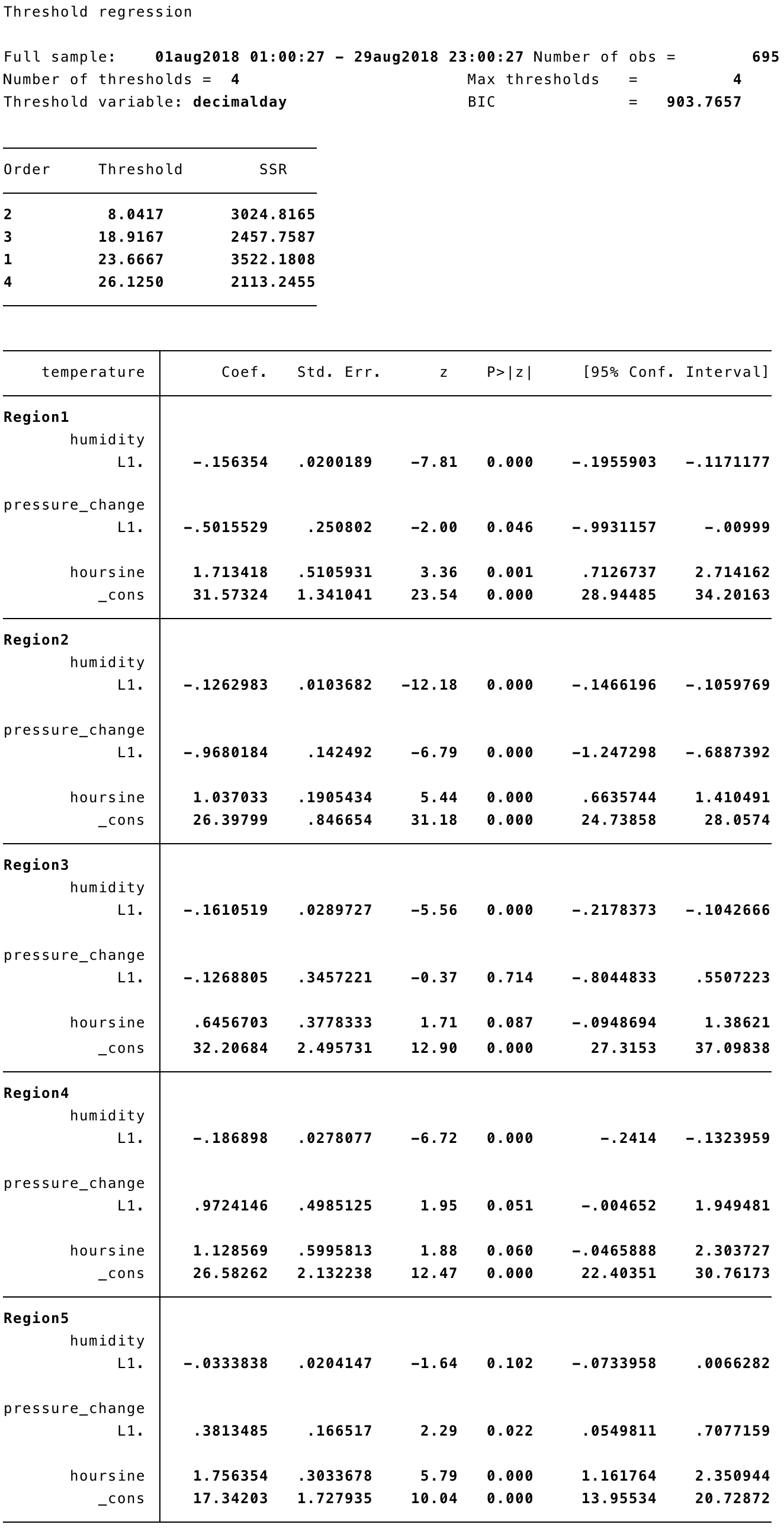
The coefficients change quite a lot, and some predictors move to having high p-values, in some of the regions. A closer examination of what this means to an expert in weather prediction would perhaps help to trim the thresholds.
How could threshold regression be used for model building in practice?
As we’ve seen, threshold regression is an exploratory technique and the final choice of model has to be taken by the analyst, taking theory into consideration alongside the stats like BIC and residual sums of squares. There is potential to overfit, especially if you set optthresh to be quite high, which is really no different to any other model building procedure. In the weather data, although I am no meteorologist, it seems justified that there is a threshold as the cold front arrives (which has been suggested in both these regressions), and perhaps another after the band of rain has passed – where there is high and aperiodic humidity in the 9-11th – (which was not suggested by threshold), replaced by colder air and showers. Beyond that, later thresholds are questionable.
The best way to guard against that is to plot your predictions and residuals and look for patterns that can refine your model. If possible, split your data into a training set (that you run threshold on), and a test set (that you apply the training set’s model to). With this cross-validation approach, you can quantify the effect of increasing optthresh.
What about non-Gaussian errors, or when the dependent variable is a count or binary?
Although threshold only tests for thresholds in linear regression (with the usual Gaussian, homoscedastic and independent errors), if you regard it as an exploratory technique pointing the way to a more detailed model, then there is no reason why you could not use it to get a selection of candidate thresholds.
Suppose you have count data and intend to fit a Poisson model. If you take logarithms (adding a small number to avoid log(0), you could run threshold and then try out the thresholds in poisson.
Non-Gaussian errors might give you incorrect standard errors but still provide reasonable coefficients and thresholds, to be properly evaluated in a more robust model. You will just have to be careful to spot any outlier residuals or clumps of outliers, that might induce a threshold where there really isn’t enough evidence to justify it, given the “true” residual distribution.
The do-file for this example can be downloaded here.